Significance of Sound Correspondences
by Ramzi Nahhas
Kessler (2001)<ref>Kessler, Brett. 2001. The Significance of Word Lists. Stanford, CA: CSLI Publications.</ref> uses a statistical method called permutation tests to test if two languages are historically related or not. His purpose is historical comparison. After reading his work, I later thought about the “three” in Blair’s statement that sound correspondences are to be considered regular if they occur three or more times in a list (Blair 1990)<ref>Blair, Frank. 1990. Survey on a Shoestring. Dallas: SIL.</ref>. This seems to be a good rule of thumb, but in fact the right number to use might not be three in all cases. It depends on the length of the word list and the frequency of occurrence of the segments in question (Blair was working with a list of length 210).
For example, suppose you find three correspondence between [s] and [z] in a list of length 500, [s] occurs in 35 of the words in the list for the first language, and [z] occurs in 25 of the words in the list for the other language. Then, even if there really were no relationship between [s] and [z], the chance of finding three or more [s] to [z] correspondences in this list is 12%. Usually, in statistics, 5% is considered to be low enough to consider “chance” less likely than a real relationship. For this situation, you would have to find four correspondences before the chance of finding so many is less than 5%. So Blair’s method in this case would have to be adjusted to only count correspondences as regular if they occur four or more times.
When counting occurrences of a segment, you need to think carefully. Should you only count the segment if it occurs in the same position (e.g. initially)? Or should you count it if it occurs in other places, as well (e.g. medially or finally)? The answer depends on what you consider to be similar environments for that language. Suppose the [s]-[z] sound correspondence reflects a process that occurs in initial segments only. Then, in that case, for this method, only count initial [s] and [z].
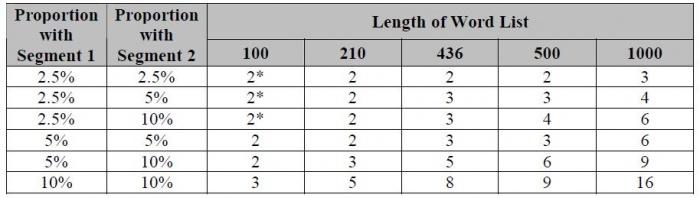
Tables 1 and 2 below provide the minimum numbers of correspondences for a variety of situations. Table 1 shows the minimum values if you consider a 5% chance low enough. Table 2 provides the minimum values if you would rather only count a set of correspondence as significant if it would occur by chance only 1% of the time.
Segment 1 and Segment 2 are the two segments for which you are testing significance (e.g. [s] and [z] in the example above). The length of the word list in these tables is the length of the whole list in which you are looking for correspondences, not just the list you are using to compute the lexical similarity percentage (these are not necessarily the same thing).
All occurrences of “1” are replaced by a “2*”. This is an example of how statistical procedures often give silly answers at the extremes. Common sense should always be applied! While, technically, 1 correspondence could be considered statistically significant under the right conditions, probably no one would really want to consider a single occurrence as “regular”. So these have been replaced by “2*”. However, you might feel the same way about 2 occurrences; that 2 are too few to be considered regular. In that case, you can just replace all the “2*” and “2” entries by 3.
Based on these results, we can say that Blair’s use of the number “3” is a pretty good rule of thumb. He could have gotten away with “2” in some situations, but perhaps he felt like two occurrences are just too few to be considered “regular”. However, for longer lists, and for more frequently occurring segments, there is a possibility that “3” is too few, that you could get three correspondences just by chance.
<references />